Biến đổi Fourier (Fourier Transform) trong xử lý ảnh

1.  Fourier transform

1.1.      Mục đích

Tìm hiểu về biến đổi Fourier và cách biểu diễn kết quả trong miền tần số.

Tìm hiểu về phép chập 1 chiều, 2 chiều, thực hiện phép chập trong miền tần số.

1.2.      Các công thức được sử dụng

Tích phân với hàm mũ:

Công thức Euler:

Từ công thức Euler có quan hệ lượng giác:

Tổng cấp số nhân:

1.3.      Biến đổi Fourier cho tín hiệu liên tục

Fourier Transform là phương pháp biến đổi tín hiệu liên tục từ miền thời gian sang miền tần số.

Công thức biến đổi Fourier như sau:

Trong đó:

• F(w) là kết quả biến đổi tín hiệu từ miền thời gian sang miền tần số.
• w là tần số góc, w = 2πf, đơn vị rad/s.
• j là biến phức (kỹ sư điện, điện tử sử dụng j thay cho i để phân biệt với ký hiệu dòng điện).
• p(t) là tín hiệu liên tục trong miền thời gian.

Ví dụ: Biến đổi Fourier cho tín hiệu

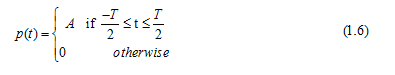
Sử dụng công thức (1.5):

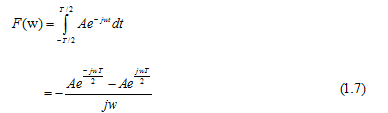
Sử dụng quan hệ (1.3) cho (1.7), thu được kết quả:

Hình 1: Tín hiệu p(t) và biến đổi Fourier

Kết quả của biến đổi Fourier có biểu diễn phức như sau:

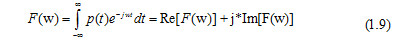
Trong đó,  Re(w) và Im(w) tương ứng là phần thực và phần ảo của biến đổi Fourier.

Giá trị biên độ (Modulus) tính như sau:

Giá trị pha (phase) tính như sau:

Có thể dùng dấu của Re(w) và Im(w) để xác định pha đang ở góc phần tư nào (do pha biến đổi từ 0 đến 2π).

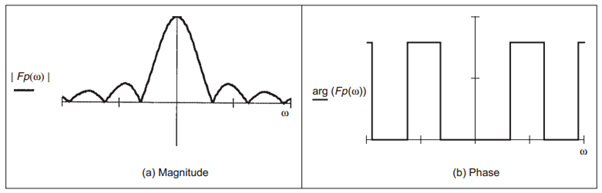
Hình 2: Biên độ và pha của F(w)

Ta có biến đổi Fourier ngược cho phép biến đổi tín hiệu từ miền tần số về miền thời gian. Phép biến đổi ngược định nghĩa theo công thức sau:

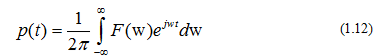
Biến đổi Fourier cho biết các tần số tạo nên tín hiệu trong miền thời gian và giá trị biên độ của tần số đó tính theo F(w). Nếu cộng tất cả các tín hiệu đó thì ta thu được tín hiệu giống hệt tín hiệu ban đầu.

Các hình sau minh họa cho quá trình tổng hợp tín hiệu p(t) trong ví dụ trên với w trong dải (-6, 6). Với dải tần càng rộng, kết quả càng giống tín hiệu ban đầu.

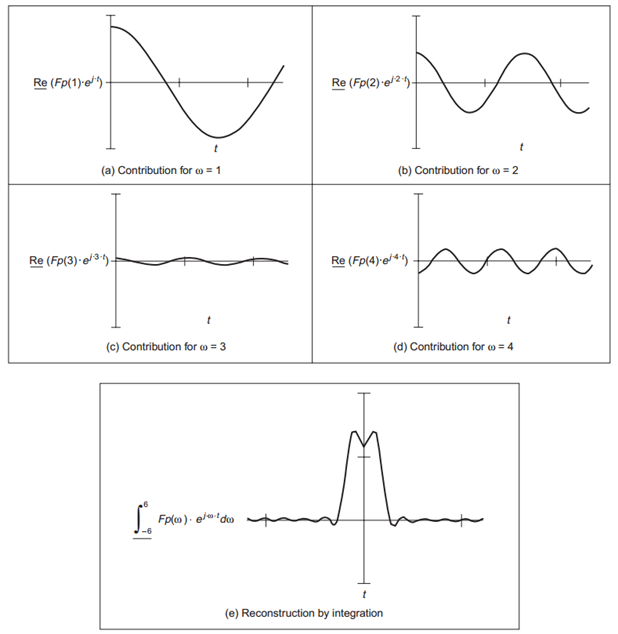
Hình 3: Tổng hợp tín hiệu

Có 1 phép toán rất quan trọng trong biến đổi Fourier đó là phép chập (Convoulution). Phép chập trong miền thời gian của tín hiệu  và tín hiệu , ký hiệu là *, định nghĩa bởi công thức sau:

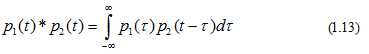
Sử dụng công thức (1.5), ta có biến đổi Fourier của phép chập như sau:

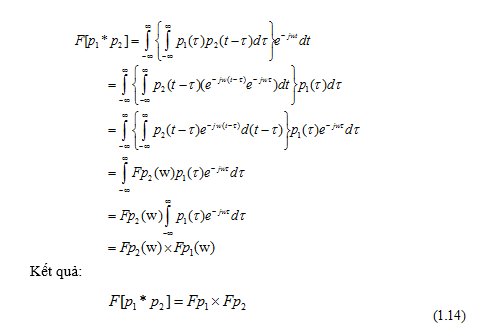
Trong đó, 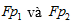  tương ứng là biến đổi Fourier của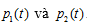  

• Thêm một cách thực hiện phép chập:
• Biến đổi tín hiệu sang miền tần số.
• Thực hiện phép nhân.
• Biến đổi ngược tín hiệu về miền thời gian.

   Cách này chỉ hiệu quả khi tín hiệu có kích thước lớn, việc thực hiện phép chập cần rất nhiều phép nhân. Chi tiết hơn sẽ được trình bày ở phần sau.

1.4.      Biến đổi Fourier rời rạc

Ảnh số là tín hiệu rời rạc. Do đó, ta cần có cách biến đổi Fourier với loại tín hiệu này, hay còn gọi là biến đổi Fourier rời rạc, viết tắt là DFT (Discrete Fourier Transform).

DFT của một tập N điểm  là một tập cá điểm  trong miền tần số, tính theo công thức sau:

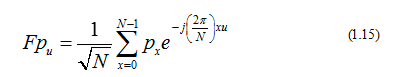
Ví dụ: Áp dụng DFT cho chuỗi tín hiệu xung  điểm có biên độ A:

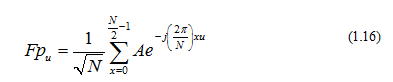
Áp dụng (1.4) cho (1.16):

Biên độ (Modulus) của số phức :

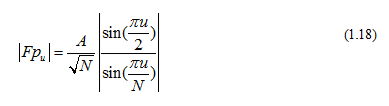
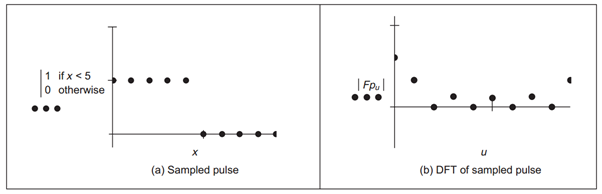
Hình 4: Hàm xung và biến đổi DFT

Tương tự như biến đổi Fourier, ta cũng có thể dùng kết quả của DFT để tổng hợp lại tín hiệu rời rạc trong miền thời gian từ các thành phần tần số dạng sin. Các hệ số của DFT cho biết biên độ của các thành phần tần số.

Công thức biến đổi DFT ngược:

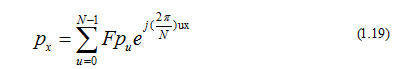
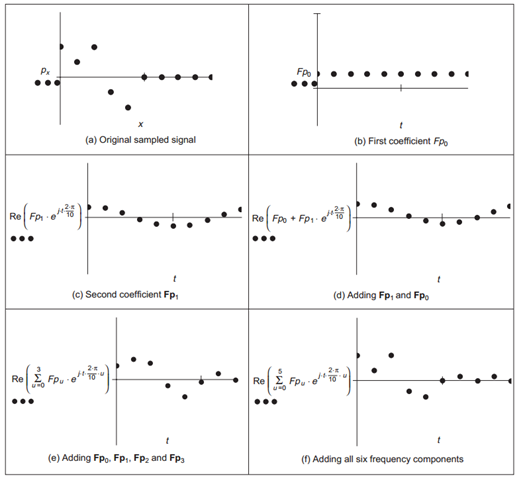
Hình 5: Tổng hợp tín hiệu  từ kết quả DFT

Bên trên ta mới chỉ xét biến đổi DFT 1 chiều. Tuy nhiên, để xử lý ảnh số, ta cần phép biến đổi DFT 2 chiều. Ta sẽ xét sự biến đổi giá trị điểm ảnh theo 2 chiều tọa độ Ox và Oy, tương ứng có 2 chiều trong miền tần số, đặt là u và v.

Biến đổi DFT cho ảnh kích thước N × N tính theo công thức sau:

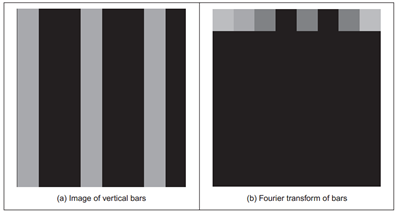
Hình 6: Biến đổi DFT 2 chiều

Hình 6 minh họa biến đổi DFT 2 chiều. Ảnh gốc chỉ có sự biến đổi giá trị theo chiều Ox nên tương ứng trong miền tần số chỉ có sự thay đổi giá trị theo u.

Giống như các biến đổi trước, DFT 2 chiều có biến đổi ngược theo công thức sau:

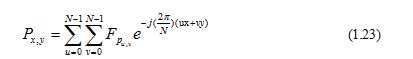
Một đặc tính quan trọng của biến đổi DFT là tính lặp lại, hay chu kỳ. Ta sẽ chứng minh DFT 2 chiều có đặc tính này. Với biến đổi DFT của ảnh kích thước N × N , với m và n là các số nguyên, ta tính:

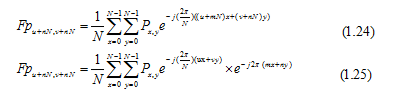
Do m, n nguyên nên  nguyên. Áp dụng (1.2) được:

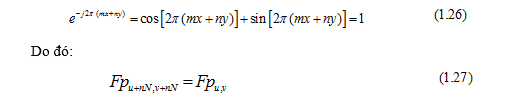
Kết quả (1.27) cho thấy 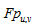 tuần hoàn với chu kỳ N, với N × N là kích thước của ảnh đầu vào.

Như vậy, mặc dù các biến u và v không bị chặn (từ -∞ đến ∞ ), nhưng do tính chất tuần hoàn nên kết quả của biến đổi DFT 2 chiều của ảnh N × N chỉ cần biểu diễn dưới dạng ma trận N × N.

Giá trị 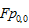 còn gọi là hệ số DC (Direct Current). Thay u = v = 0  vào phương trình (1.17) ta được:

 

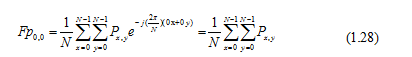
Hay 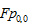 là tổng giá trị tất cả các điểm ảnh chia cho .

Hình 7 bên trái biểu diễn kết quả biến đổi DFT dưới dạng ma trận. Ta sử dụng phép dịch để được kết quả như hình bên phải, điểm tần số 0 (hệ số DC) nằm ở giữa ma trận, các điểm biểu diễn tần số tăng dần theo chiều tiến ra biên.

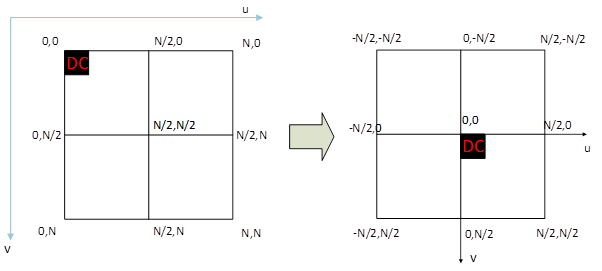
Hình 7: Dịch hệ số DC vào giữa ma trận kết quả

Phương trình (1.29) cho thấy khi nhân mỗi điểm ảnh với 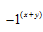, điểm biểu diễn DFT bị dịch đi một đoạn  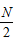theo cả 2 trục. Tức là điểm tần số 0 sẽ nằm chính giữa ma trận kết quả biểu diễn miền tần số.

Thực tế là biến đổi DFT theo định nghĩa khá chậm khi thực hiện trên ảnh có kích thước lớn do phải thực hiện rất nhiều phép nhân. Biến đổi DFT thường được thực hiện bằng thuật toán Fast Fourier Transform (FFT) giúp cải thiện rất nhiều khối lượng tính toán. Tài liệu này không trình bày chi tiết FFT.

Ví dụ: Tính DFT 1 chiều cho tín hiệu rời rạc có 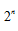 phần tử cần tới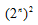 

 phép nhân. Tuy nhiên, FFT chỉ cần n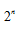  . Do đó, tốc độ xử lý tăng  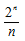lần.

Bảng 1: So sánh thực hiện DFT theo định nghĩa và sử dụng FFT

Kích thước (2n)	Số phép nhân		Tỉ lệ (Định nghĩa/FFT)
	Định nghĩa	FFT
4	16	8	2.0
8	84	24	2.67
16	256	64	4.0
32	1024	160	6.4
64	4096	384	10.67
128	16384	896	18.3
256	65536	2048	32.0
512	262144	4608	56.0
1024	1048576	10240	102.4

Phép chập giữa 2 ảnh A và B, hay chập 2 chiều, định nghĩa theo công thức sau:

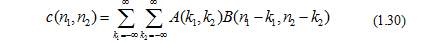
Phép chập này được sử dụng rất nhiều trong xử lý ảnh. Nó chính là cách sử dụng mặt nạ để lọc biên (Sobel, Prewit, Robert), nhiễu , lọc thông thấp thông cao (Gaussian). Giống như chập tín hiệu 1 chiều, phép chập tín hiệu 2 chiều trong miền thời gian tương đương phép nhân trong miền tần số.

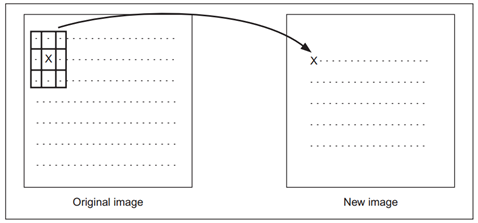
Hình 8: Phép chập trong xử lý ảnh

Lưu ý: Như đã đề cập ở trên, kết quả của phép DFT thường chỉ biểu diễn dạng ma trận   N × N, với N × N là kích thước ảnh. Nhưng trong miền tần số, u và v không bị giới hạn và kết quả DFT có tính lặp lại theo N.

Giả sử ta cần lọc ảnh N × N sử dụng mặt nạ m × n. Độ phức tạp của FFT 2 chiều là 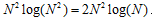. Nếu mặt nạ dùng để lọc đã được biến đổi trước thì ta chỉ cần dùng FFT 2 lần. Sau đó, cần N² phép nhân để nhân 2 ảnh và mặt nạ trong miền tần số. Tổng hợp độ phức tạp:

Thực hiện lọc theo định nghĩa cần  phép nhân cho mỗi điểm ảnh. Số phép nhân cho toàn bộ quá trình lọc theo định nghĩa là:

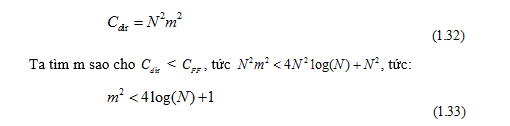
Ví dụ: Với ảnh kích thước 256×256, ta sử dụng chập trực tiếp với bộ lọc có mặt nạ kích thước 3×3, 5×5 hoặc 7×7. Với mặt nạ lớn hơn, sử dụng FFT cho kết quả nhanh hơn.

2.  Ứng dụng Fourier transform

2.1.      Bộ lọc thông thấp, thông cao

Ta đã biết, trong ảnh xám, vùng ảnh mà giá trị giữa các Pixel thay đổi đột ngột là vùng ảnh tần số cao, ví dụ như biên hoặc nhiễu. Ngược lại, vùng ảnh mà giá trị các Pixel thay đổi rất ít là vùng ảnh có tần số thấp, ví dụ như vùng nền (Background).

Giả sử, ta có ma trận kết quả biến đổi DFT của 1 ảnh xám, hệ số DC được dịch vào giữa. Do các thành phần tần số thấp ở gần tâm ma trận, ta có thể thực hiện các bộ lọc tần số thấp bằng cách loại bỏ các hệ số ở cách xa tâm.

Hình 9: Ảnh xám (trái) và biến đổi DFT (phải)

Hình 10: Lọc thông thấp (trái) và kết quả (phải)

Hình trên minh họa lọc thông thấp trong miền tần số. Với kích thước hình tròn càng nhỏ thì hình càng bị mờ do các thành phần tần số cao bị lọc đi nhiều.

Hình 11: Lọc thông thấp với các kích thước bộ lọc

Ngược lại với lọc thông thấp. Lọc thông cao sẽ loại bỏ các hệ số ở gần tâm và giữa lại các hệ số cách xa tâm. Với kích thước hình tròn càng lớn thì biên của đối tượng trong ảnh càng hiện rõ. Tuy nhiên, bộ lọc này không lọc được nhiễu.

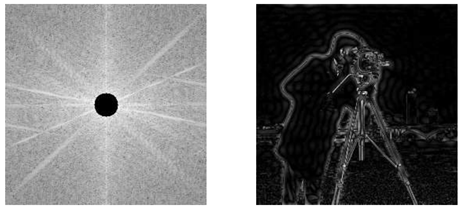
Hình 12: Lọc thông cao (trái) và kết quả (phải)

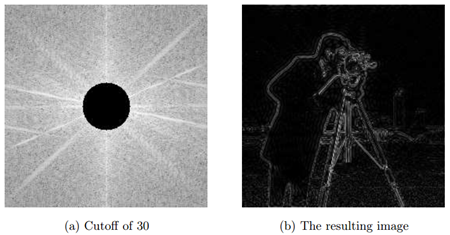
Hình 13: Lọc thông cao với kích thước lớn hơn