Tìm hiểu về Contour, moments trong xử lý ảnh

1.    Mục tiêu

Tìm hiểu về thuật toán contour, moment và ứng dụng trong xử lý ảnh số.

2.    Thuật toán contour

2.1.     Giới thiệu

Contour là thuật toán được sử dụng trong xử lý ảnh nhằm tách, trích xuất các đối tượng, tạo điều kiện để các xử lý sau được chính xác. Nên threshold or canny edge detection trước khi sử dụng thuật toán này.

Hình  1: Ví dụ về thuật toán contour

⇒ Rất hữu ích trong việc shape analysis and object detection and recognition.

2.2.     Một số khái niệm

Neighbor: 2 pixel được gọi là neighbor nếu 2 pixel đó chung một cạnh.

Thành phần connected: giả sử trong ảnh binary, các pixel thuộc 1 đối tượng có giá trị 1 còn các pixel thuộc nền thì có giá trị 0. Lúc này nếu giữa 2 pixel bất kì thuộc đối tượng, chuỗi các pixel thỏa mãn:

• Tất cả đều thuộc đối tượng, tức là các pixel này có giá trị bằng 1.
• Mỗi pixel thuộc chuỗi đều phải neighbor với pixel trước và kế tiếp trong chuỗi.

thì chuỗi pixel đó được gọi là một thành phần connected.

4-connectivity: xem hình 2, P với P2 là một 4-connectivity, tương tự P với P4, P với P6 hay P với P8 đều là một 4-connectivity.

4-connected: một đối tượng được gọi là 4-connected nếu thỏa mãn: bất kỳ 2 pixel liền kề nhau thuộc đối tượng là một 4-connectivity.

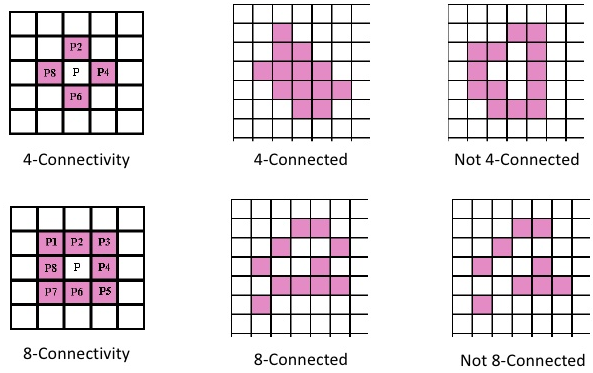
Hình  2: Ví dụ về 4-connectivity và 8-connectivity

8-connectivity: xem hình 2, P với bất kì pixel nào xung quanh nó đều tạo nên một 8-connectivity.

8-connected: một đối tượng được gọi là 8-connected khi thỏa mãn: bất kỳ 2 pixel liền kề nhau thuộc đối tượng là một 8-connectivity.

2.3.     Contour Tracing Algorithms

Có 4 thuật toán thông dụng nhất được sử dụng trong contour tracking, gồm:

• Square Tracing Algorithm.
• Moore – Neighbor Tracing.
• Radial Sweep.
• Theo Pavlidis’ Algorithm.

Trong số đó, Square Tracing Algorithm và Moore – Neighbor Tracing dễ triển khai nên được sử dụng phổ biến hơn cả.

2.3.1.     Square Tracing algorithm

Thuật toán: Duyệt từ pixel ngoài cùng bên trái phía dưới, đi lên cho tới khi gặp pixel có giá trị bằng 1 (pixel này sẽ được gọi là pixel start) thì bắt đầu di chuyển theo quy tắc sau:

• Nếu gặp Pixel có giá trị bằng 1 thì rẽ trái.
• Nếu gặp Pixel có giá trị bằng 0 thì rẽ phải.
• Di chuyển cho tới khi quay lại pixel start thì dừng lại.

Hình sau mô tả cách hoạt động của thuật toán:

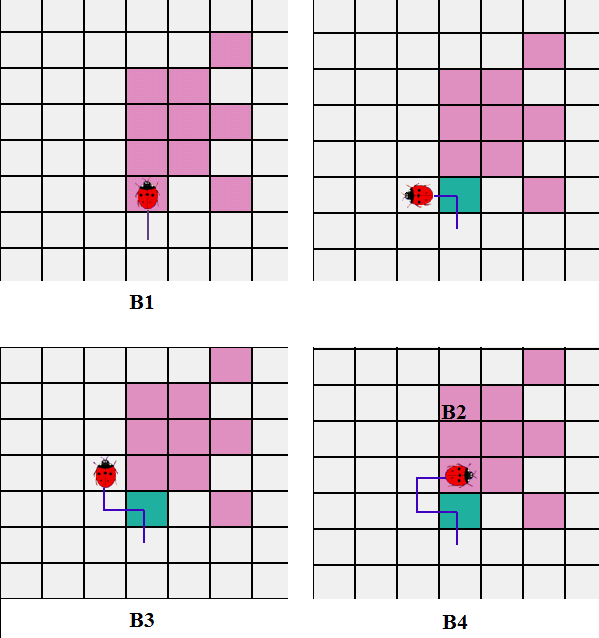
Hình  3: Mô tả quá trình tìm contour của thuật toán Square Tracing

Điều kiện kết thúc:

Thuật toán kết thúc khi gặp một trong hai điều kiện sau:

• Di chuyển vào pixel start lần thứ 2 sau khi đi qua n pixel khác. Nếu điều kiện này xảy ra, có nghĩa rằng thuật toán chạy sai, xem ví dụ như hình 4.

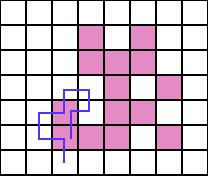
Hình  4: Ví dụ trường hợp thuật toán chạy sai

• Di chuyển vào pixel start lần thứ 2 sau khi đi qua n pixel khác và theo đúng hướng đi vào pixel start lần đầu tiên, điều kiện này còn được gọi là Jacob’s stopping criterion. Điều kiện này xảy ra nghĩa là thuật toán đã chạy đúng, như ví dụ ở hình 5. Vậy thuật toán chỉ chạy đúng trên đối tượng 4-connected.

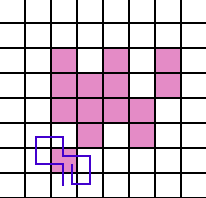
Hình  5: Ví dụ trường hợp thuật toán chạy đúng

2.3.2.     Moore – Neighbor Tracing

Thuật toán: Moore – Neighbor tracking có chút khác biệt só với thuật toán Square Tracking, cụ thể: khi gặp pixel có giá trị bằng 1 đầu tiên (pixel start) thì ta sẽ quay lại pixel trước đó, sau đó đi vòng qua các pixel thuộc 8-connected theo chiều kim đồng hồ cho tới khi gặp pixel khác có giá trị bằng 1.

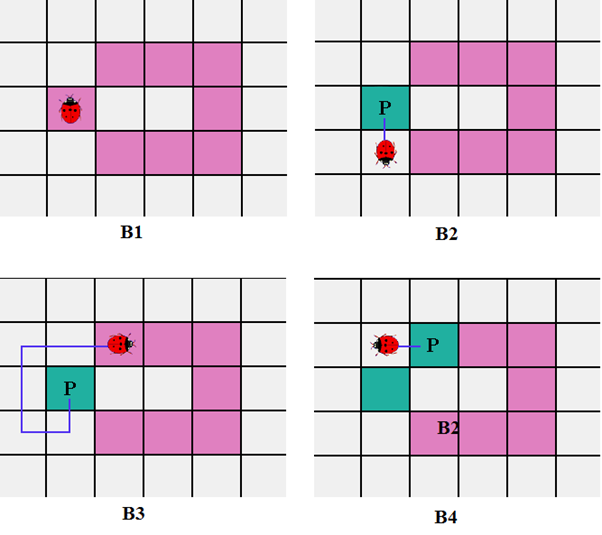
Hình  6: Mô tả quá trình tìm contour của thuật toán Moore-Neighbor Tracking

Điều kiện kết thúc: Giống với thuật toán Square Tracking.

2.3.3.     Radial Sweep

Thuật toán: Cũng giống với Moore – Neighbor Tracking, sau khi gặp pixel có giá trị bằng 1 đầu tiên (Start pixel), ta sẽ quay lại pixel trước đó và đi vòng theo chiều kim đồng hồ cho tới khi gặp pixel có giá trị bằng 1 tiếp theo, lúc này Radial Sweep sẽ không thực hiện như Moore-Neighbor Tracking, mà thay vào đó, nó tạo ra một đoạn thẳng ảo nối pixel hiện tại với pixel có giá trị bằng 1 đã đi qua gần nhất. Và đoạn thẳng này được xoay cho tới khi gặp một pixel khác có giá trị bằng 1. Xem hình 7 để hiểu rõ hơn về thuật toán.

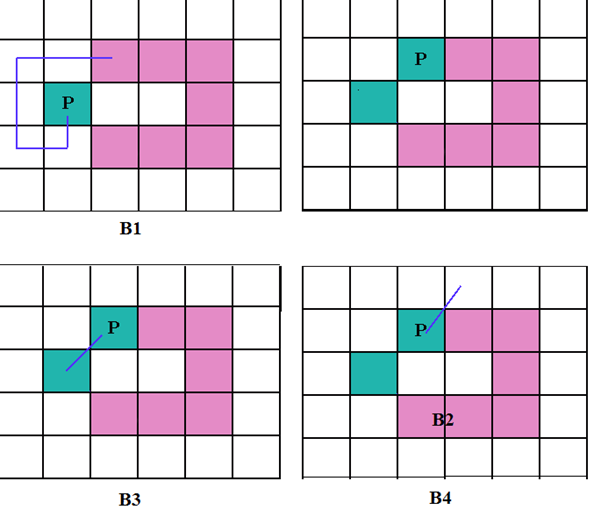
Hình  7: Mô tả quá trình tìm contour của thuật toán Radial Sweep

Điều kiện kết thúc: Giống với thuật toán Square Tracking.

2.3.4.     Theo Pavlidis’ Algorithm

Thuật toán: Tại pixel start, 3 điểm P1, P2, P3 được định nghĩa như hình 8a. Lúc này việc lựa chọn P1, P2, hay P3 làm điểm đến tiếp theo được xét như sau:

• Nếu P1 có giá trị bằng 1 thì P1 được chọn là điểm kế tiếp, quá trình di chuyển được mô tả như hình 8b.
• Nếu P1 có giá trị bằng 0, thì P2 được xét, nếu P2 có giá trị bằng 1 thì P2 được chọn và quá trình di chuyển được mô tả như hình 8c.
• Nếu P1, P2 đều có giá trị bằng 0 thì P3 được xét, nếu P3 có giá trị bằng 1 thì P3 được chọn và quá trình di chuyển được mô ta như hình 8d.
• Nếu cả P1, P2 và P3 đều không thỏa mãn thì ta sẽ quay 90^o theo chiều kim đồng hồ để được 3 vị trí P1, P2 và P3 mới.

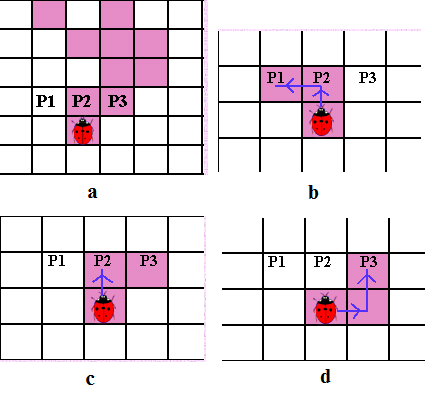
Hình  8: Mô tả quá trình tìm contour của thuật toán Theo Pavlidis’ Algorithm

Điều kiện kết thúc:

Thuật toán kết thúc khi gặp một trong 2 điều kiện sau:

• Di chuyển tới start pixel lần thứ 2.
• Khi chuyển hướng 3 lần mà vẫn không tìm được pixel thỏa mãn.

3.    Thuật toán moment

3.1.     Giới thiệu

Moment là thuật toán giúp đánh giá sự giống nhau của 2 đối tượng; sử dụng trong các phép biến đổi translate, scaling hay rotate; hay sử dụng các khối hình học để tái xây dựng lại đối tượng.

3.2.     Thuật toán

Công thức xác định moment như sau:

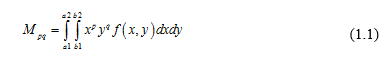
Trong đó:

• p, q = 0, 1, 2,…
• f(x, y) là giá trị tại pixel có tọa độ (x, y).

Moment được phân biệt nhờ vào 2 tham số p và q, giá trị (p + q) là thứ tự của moment đó và được ký hiệu là m_p,q. Cụ thể một số moment được định nghĩa như sau:

• m_0,0 được gọi là zero order moment, moment này chính là diện tích của đối tượng.
• m_0,1 hay m_1,0 được gọi là first order moments, contain information about the center of gravity of the object.
• m_2,0, m_0,2 hay m_1,1 được gọi là second order moments.
• …

3.2.1.     Moment Invariants

Translate, rotation and scaling (TRS) là những phép biến đổi đơn giản trong không gian. TRS thỉnh thoảng được gọi là biến đổi similarity, gồm 4 tham số được biểu diễn bằng công thức sau:

Trong đó:

• t là translate vector.
• s là positive scaling factor (note that here we consider uniform scaling only, s is the same, both in horizontal and vertical direction).
• R là rotate matrix

Với α là góc quay.

Bất biến trong TRS là một yêu cầu quan trọng trong mọi ứng dụng. Bởi vì đối tượng nên được xác định chính xác vị trí trong bức ảnh. Vì vậy TRS invariants trở nên quan trọng. Translation and scaling invariants có thể khá trực quan nhưng invariants to rotation thì phức tạp hơn.

Invariants to translation:

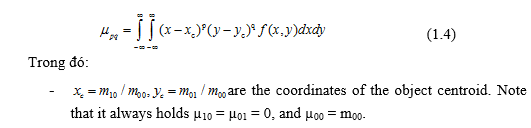
Invariants to uniform scaling:

Moment sử dụng trong scaling normalization không còn được sử dụng trong nhận dạng vì giá trị của the corresponding normalized moment luôn luôn bằng 1(in the above normalization, ν₀₀ = 1).

Traditional invariants to rotation:

Được giới thiệu lần đầu vào năm 1962 bởi Hu, ông đã định nghĩa ra 7 công thức sau

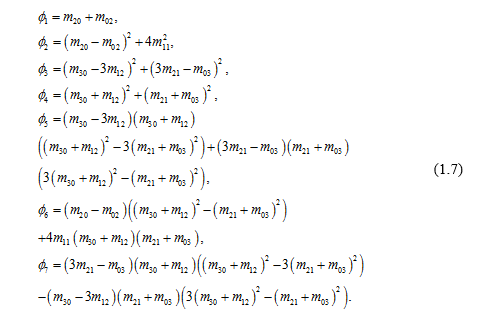
3.2.2.     Complex moment

Công thức:

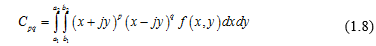
Trong miền tọa độ cực, công thức có thể viết lại như sau:

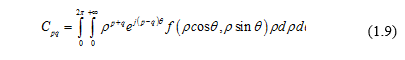
Nếu complex moment của ảnh gốc với complex moment của ảnh rotate được ký hiệu lần lượt là 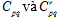 thì mối quan hệ giữa chúng là:

Với θ là góc quay