Khái niệm cơ bản về xử lý ảnh Computer Vision và các phép toán trong xử lý ảnh.
1. Xử lý điểm ảnh
1.1. Mục tiêu
Tìm hiểu các khái niệm cơ bản của ảnh số như Pixel, Grayscale, Histogram. Các kỹ thuật xử lý điểm ảnh như sử dụng Threshold, sử dụng các bộ lọc.
1.2. Pixel
Pixel viết tắt của từ Picture Element hay phần tử của bức ảnh. Một ảnh số là một tập hợp của các Pixel.
Ảnh trong thực tế được số hóa do đó giá trị của nó không liên tục mà rời rạc trong quá trình lấy mẫu. Khi được số hóa, ảnh được biểu diễn bởi mảng hai chiều gồm n dòng và p cột, hay ta nói ảnh gồm n x p pixel. Mỗi pixel gồm một cặp tọa độ và giá trị màu. Giá trị màu có thể lưu trữ trên 1, 4, 8 hay 24 bit.
Ví dụ như ảnh RGB dùng 24 bit để lưu 1 Pixel, trong đó mỗi màu Red, Green, Blue chiếm 8 bit.
1.3. Mức xám (Gray level)
Mức xám là kết quả của sự mã hóa tương ứng một cường độ sáng của mỗi điểm ảnh với một giá trị số. Thường dùng 8 bit để mã hóa 256 mức xám.
Hình 1: Các mức xám
Để chuyển ảnh màu RGB sang ảnh xám, áp dụng công thức cho mỗi Pixel:
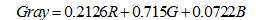
Công thức trên dựa trên sự nhạy cảm của mắt người với 3 màu RGB.
1.4. Histogram
Cho một kênh ảnh đa mức. Histogram là biểu đồ mô tả số điểm ảnh tương ứng với mỗi mức. Ta hay sử dụng ảnh đa mức xám để lập biểu đồ Histogram.
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig2.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig2.png?w=736)
Hình 2: Ảnh trước cân bằng Histogram
Histogram thể hiện độ tương phản sáng tối của ảnh chụp. Ảnh bên trên có các điểm ảnh chỉ tập trung vào một vùng mức xám, do đó ảnh bị tối. Tăng độ tương phản bằng thuật toán cân bằng Histogram.
Thuật toán Histogram: Giả sử ảnh có L mức xám 0,1,2,…, (L-1). Có điểm ảnh có mức xám i. Tổng số điểm ảnh là 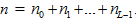 . Ta thay đổi giá trị các điểm ảnh có mức xám i bằng giá trị mức xám nguyên gần nhất với
. Ta thay đổi giá trị các điểm ảnh có mức xám i bằng giá trị mức xám nguyên gần nhất với
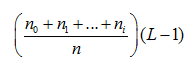
Kết quả ảnh thu được có độ tương phản tốt hơn, giá trị các điểm ảnh trải đều trên các mức.
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig3.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig3.png?w=736)
Hình 3: Kết quả cân bằng Histogram
1.5. Xử lý theo ngưỡng (Thresholding)
Xử lý ngưỡng sử dụng 1 giá trị ngưỡng (trong khoảng 0 – 255) để xử lý 1 kênh màu hoặc ảnh đa mức xám. Kết quả nhận được là ảnh nhị phân, tức là có thể biểu diễn 1 pixel bằng 1 bit.
Ngưỡng đơn: xử lý 1 ảnh đa mức xám thành ảnh nhị phân (đen trắng) bằng cách so sánh giá trị điểm ảnh với một ngưỡng T cố định. Nếu giá trị điểm ảnh lớn hơn T thì gán điểm ảnh màu trắng và ngược lại.
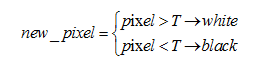
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig4](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig4.png?w=736)
Hình 4: Xử lý ngưỡng ảnh xám (trái) và kết quả (phải)
Ngưỡng kép: sử dụng 2 ngưỡng 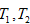 như sau:
như sau:
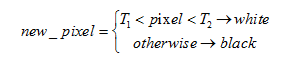
Kết quả:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig5.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig5.png?w=736)
Hình 5: Xử lý ngưỡng kép ảnh xám (trái) và kết quả (phải)
Ứng dụng của thresholding:
- Phân mảnh ảnh.
- Tách vật thể khỏi nền.
- Loại bỏ các chi tiết không cần thiết.
- Hiện lên các chi tiết ẩn hoặc mờ.
1.6. Lọc không gian (Spatial filter)
Lọc không gian là cách xử lý một điểm ảnh có sự ảnh hưởng của các điểm ảnh xung quanh nó.
Ta dùng một mặt nạ (mask), di chuyển mặt nạ trên toàn bộ bề mặt ảnh và thực hiện 1 phép xử lý các điểm ảnh nằm trong mặt nạ. Trên mặt nạ được đánh dấu một điểm gọi là nhân. Kết quả của phép xử lý sẽ được gán cho điểm trên ảnh trùng với nhân. Các mặt nạ thường có kích thước lẻ và nhân nằm ở giữa mặt nạ để kết quả xử lý phụ thuộc đều cả hai phía.
Các phép toán có thể là tuyến tính, ví dụ như nhân các điểm ảnh với phần tử tương ứng trên mặt nạ rồi cộng dồn lại và gán cho điểm ảnh ở tâm mặt nạ.
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig6.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig6.png?w=736)
Hình 6: Minh họa lọc không gian
Một vấn đề là khi thực hiện lọc tại vùng biên ảnh, 1 phần mặt nạ sẽ bị dôi ra ngoài.
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig7.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig7.png?w=94)
Hình 7: Mặt nạ tại biên ảnh
Lúc đó, ta có thể xử lý theo 1 trong các cách sau, tuy nhiên có sai số.
- Không lọc biên. Ta chỉ sử dụng mặt nạ khi nó nằm khít bên trong ảnh. Toàn bộ các điểm ảnh ở biên sẽ không được lọc và ảnh kết quả sẽ có kích thước nhỏ hơn so với ảnh đầu vào. Nếu mặt nạ có kích thước lớn thì sẽ có nhiều điểm ảnh bị mất.
- Đệm điểm ảnh không. Khi mặt nạ ở biên, ta sẽ đệm các điểm ảnh 0 vào phần mặt nạ bị dôi. Khi đó, toàn bộ điểm ảnh được lọc và kích thước ảnh được giữ nguyên. Tuy nhiên, phần biên ảnh cho kết quả không chính xác và có thể gây ảnh hưởng tới các bước xử lý tiếp theo.
Vấn đề tiếp theo là giá trị điểm ảnh kết quả có thể nằm ngoài khoảng [0 – 255] .
Khi đó, ta có thể dùng 1 vài cách như sau:
- Lấy trị tuyệt đối các giá trị âm.
- Chặn giá trị. Giả sử điểm ảnh nhận được sau lọc là x, xử lý x:
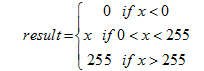
- Biến đổi dải kết quả theo tỉ lệ. Giả sử sau khi lọc toàn bộ ảnh, giá trị điểm ảnh nhỏ nhất là
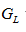 và lớn nhất là
và lớn nhất là 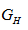 . Thực hiện chuyển đổi giá trị x trong dải
. Thực hiện chuyển đổi giá trị x trong dải 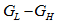 thành y trong dải 0 – 255 theo công thức:
thành y trong dải 0 – 255 theo công thức:
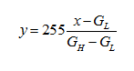
1.7. Tần số và các bộ lọc thông thấp, thông cao
Định nghĩa tần số: Tần số định nghĩa bởi sự thay đổi mức xám của theo khoảng cách (tính theo số điểm ảnh).
Thành phần tần số cao xuât hiện tại vùng có sự thay đổi lớn giữa 1 khoảng cách nhỏ. Ví dụ như biên vật thể hoặc nhiễu.
Ngược lại, thành phần tần số thấp xuất hiện tại vùng có sự thay đổi nhỏ mức xám giữa khoảng cách lớn. Ví dụ như nền ảnh.
Từ định nghĩa, ta có các bộ lọc như sau:
- Lọc thông cao (high pass filter): Cho phép các thành phần tần số cao đi qua, loại bỏ hoặc giảm bớt các thành phần tần số thấp.
- Lọc thông thấp (low pass filter): Cho phép các thành phần tần số thấp đi qua, loại bỏ hoặc giảm bớt các thành phần tần số cao.
Các bộ lọc tần số biểu diễn dạng mặt nạ. Ví dụ mặt nạ cho bộ lọc thông cao:
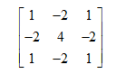
Để ý tổng các phần tử trong mặt nạ thường xấp xỉ hoặc bằng 0. Có nghĩa là khi mặt nạ di chuyển tới vùng tần số thấp (các điểm ảnh có giá trị xám xấp xỉ nhau) thì điểm ảnh kết quả có giá trị gần 0.
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig8.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig8.png?w=736)
Hình 8: Lọc thông cao với các vùng ảnh thông thấp
Bộ lọc thông cao dùng trong lọc biên hoặc làm rõ biên. Bộ lọc thông thấp dùng để khử nhiễu, làm mờ ảnh.
1.8. Nhiễu (Noise)
Nhiễu là khái niệm chỉ sự suy giảm chất lượng tín hiệu ảnh do nguyên nhân từ các tác động bên ngoài gây ra, như trong quá trình truyền dẫn tín hiệu có thể xảy ra lỗi. Như vậy việc xoá, giảm số lượng các tín hiệu nhiễu là một việc quan trọng trong xử lý ảnh.
Nhiễu muối (Salt and pepper noise) là loại nhiễu mà các tín hiệu trắng, hoặc đen, hoặc cả 2 xuất hiện ngẫu nhiên trong ảnh.
Loại nhiễu này chỉ xảy ra ở các tín hiệu tần số cao nên có thể sử dụng bộ lọc thông thấp để xử lý nhiễu, kích thước bộ lọc có thể là 3×3, 5×5 hay 7×7. Kết quả cho thấy kích thước bộ lọc 7×7 cho kết quả tốt hơn. Tuy nhiên, ảnh sẽ bị mờ đi do các cạnh của vật thể bị lọc bớt. Hình dưới cho thấy kết quả lọc chưa được tốt.
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig9.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig9.png?w=736)
Hình 9: Nhiễu muối
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig10.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig10.png?w=736)
Hình 10: Kết quả sử dụng với bộ lọc thông thấp 3×3 và 7×7
Để lọc nhiễu muối tốt, ta dùng bộ lọc trung vị (Medial filtering). Bộ lọc trung vị sắp xếp giá trị các điểm ảnh trong mặt nạ theo thứ tự rồi chọn phần tử ở giữa làm kết quả. Trong trường hợp số điểm ảnh chẵn, kết quả là trung bình của 2 giá trị ở giữa.
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig10.2](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig10-2.png?w=736)
Hình 10: Bộ lọc trung vị
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig11.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig11.png?w=736)
Hình 11: Kết quả lọc trung vị
Có thể coi bộ lọc trung vị là bộ lọc thông thấp phi tuyến do bộ lọc này làm mờ các đường biên.
1.9. Xác định biên vật thể
Biên vật thể cho biết nhiều thông tin, ta dùng biên để ước lượng chiều dài đối tượng, tách vật thể ra khỏi nền. Có rất nhiều thuật toán tìm biên sử dụng bộ lọc.
Tìm biên thực chất là quá trình lọc sự thay đổi đột ngột giá trị mức xám của các pixel gần nhau.
Ví dụ: Ta có dãy pixel như sau
20, 20, 20, 20, 20, 100, 180, 180, 180, 180, 180
Nếu ta tìm sự sai khác bằng cách trừ pixel sau cho pixel trước, ta được
0, 0, 0, 0, 80, 80, 0, 0, 0 ,0
Để tìm sự sai khác trong 1 bức ảnh theo chiều ngang, ta có thể dùng bộ lọc có mặt nạ như sau: 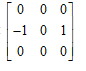
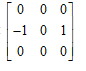
Tuy nhiên, kết quả sẽ không được mượt. Ta sử dụng thêm bộ lọc sau để làm mượt theo chiều dọc: 

Tổng hợp 2 bộ lọc trên, ta được bộ lọc Prewitt, theo cả 2 chiều:
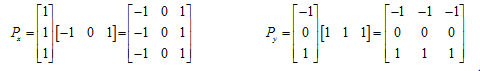
Ta phải sử dụng cả 2 bộ lọc này để lọc biên theo phương ngang và dọc. Sau đó, tổng hợp 2 kết quả thu được. Giả sử px, py là 2 ảnh thu được sau lọc. Sử dụng 1 trong 3 cách sau để tổng hợp kết quả cuối cùng:
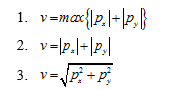
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig12.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig12.png?w=736)
Hình 12: : Ảnh trước khi lọc biên
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig13.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig13.png?w=736)
Hình 13: Lọc biên theo chiều ngang và dọc
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig14.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig14.png?w=736)
Hình 14: Kết quả lọc biên Prewitt
Bộ lọc biên Sobel tương tự như Prewitt, các mặt nạ của bộ lọc Sobel:

![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig15.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig15.png?w=736)
Hình 15: Kết quả lọc biên sobel
2. Biến đổi ảnh
2.1. Biến đổi Hough (Hough transform)
Biến đổi Hough thường dùng để xác định đường thẳng hoặc vòng tròn trong ảnh đã được nhị phân hóa.
Thông thường, 1 đường thẳng có biểu diễn toán học dạng . 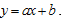
Như vậy, với mỗi cặp tọa độ (x, y) cho trước, luôn có 1 họ đường thẳng đi qua nó. Tuy nhiên, cách biểu diễn này rất khó để xác định 1 đường thẳng đi qua nhiều điểm trong 1 bức ảnh do không giới hạn được giá trị a và b.
Ta có 1 cách biểu diễn khác như sau:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig16.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig16.png?w=736)
Hình 16: Biểu diễn đường thẳng bởi r θ
Như hình trên, một đường thẳng được đặc trưng bởi góc (-90 < θ < 90) so với trục x và khoảng cách r tới điểm gốc (0, 0). Với mỗi điểm ảnh (x, y), đường thẳng qua nó được biểu diễn như sau:
Như vậy, việc biểu diễn đường thẳng bằng các cặp giá trị (a, b) được biến đổi thành biểu diễn giá trị r trong miền θ dưới dạng đường cong dạng sin. Cách này gọi là biến đổi Hough.
Áp dụng biến đổi Hough để tìm đường thẳng trong ảnh nhị phân. Với mỗi điểm ảnh trắng, ta có 1 cặp tọa độ (x, y), tương ứng là đường cong biểu diễn giá trị r trong miền θ. Tìm giao của 2 đường cong cho ta (r, θ) biểu diễn đường thẳng đi qua 2 điểm. Ta có thể đặt giá trị ngưỡng N cho số đường cong đi qua điểm (r, ) bất kỳ và chọn kết quả là các cặp (r, θ) có số đường cong đi qua lớn hơn N.
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig17.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig17.png?w=113)
Hình 17: Biểu diễn giá trị r trong miền θ
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig18.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig18.png?w=736)
Hình 18: Vẽ đường thẳng theo r và θ
3. Xử lý hình thái học
Xử lý hình thái học rất hữu dụng trong việc phân tích các khối hình trong ảnh, tuy nhiên phương pháp này chỉ áp dụng với ảnh nhị phân.
3.1. Di chuyển (Translation)
Phép di chuyển tập điểm ảnh nhị phân A sang tọa độ w(x, y). Ký hiệu
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig19.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig19.png?w=736)
Hình 19: Di chuyển A theo ω
Lưu ý: Tập điểm ảnh là các điểm ảnh trắng trên nền đen hoặc ngược lại.
3.2. Phản chiếu (Reflection)
Nếu A là tập các điểm ảnh nhị phân thì phản chiếu của A, ký hiệu 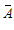 , là
, là
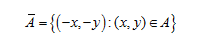
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig20.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig20.png?w=736)
Hình 20: Phản chiếu của A
3.3. Giãn nở (Dilation)
Giả sử A và B là tập các điểm ảnh nhị phân. Sự giãn nở của A bởi B, ký hiệu A⊕B định nghĩa như sau:
Tức là với mỗi điểm ảnh của B, ta phải thực hiện phép di chuyển A theo giá trị tọa độ điểm ảnh. Sau đó, hợp tất cả các kết quả lại.
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig21.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig21.png?w=736)
Hình 21 Giãn nở ảnh
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig22.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig22.png?w=736)
Hình 22: Giãn nở ảnh nhị phân làm rõ chữ
3.4. Xói mòn (Erosion)
Ngược lại với giãn nở là xói mòn. Ký hiệu 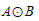 .
.
Với A, B là 2 tập điểm ảnh. Di chuyển B trên toàn bề mặt A. Nếu các điểm ảnh trên B trùng với điểm ảnh trên A, ta đánh dấu vị trí điểm ảnh tương ứng với B(0, 0). Tập các điểm được đánh dấu là kết quả xói mòn A bởi B.
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig23.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig23.png?w=736)
Hình 23: Xói mòn A bởi B
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig24.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig24.png?w=736)
Hình 24: Xói mòn trong ảnh nhị phân
3.5. Kết hợp giữa giãn nở và xói mòn
Thức hiện các phép toàn giãn nở và xói mòn cho phép ta thay đổi kích thước của vật thể trong ảnh nhị phân. Thực hiện phép trừ giữa A, A⊕B và 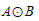 cho ta đường bao của vật thể. Ta có thể sử dụng các phép trừ sau:
cho ta đường bao của vật thể. Ta có thể sử dụng các phép trừ sau:
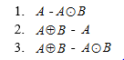
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig25.2.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig25-2.png?w=736)
Hình 25: 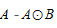
3.6. Mở (Opening)
Openning là phép toán cao cấp sử dụng xói mòn theo sau là giãn nở.
Với A, B là 2 tập điểm ảnh, ký hiệu Opening: 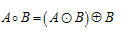
Opening thực chất là quá trình tìm và giữ lại trên A các nhóm điểm ảnh có thể trùng khít với tập điểm ảnh trên B.
Đầu tiên thực hiện xói mòn trên A. Các nhóm điểm ảnh giống B bị xói mòn còn lại nhân. Sau đó giãn nở, mỗi điểm nhân trên tạo ra một tập ảnh trùng với B trên A.
Ví dụ:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig26.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig26.png?w=736)
Hình 26: : Opening
Một vài tính chất của Opening:

3.7. Đóng (Closing)
Ngược với Opening, Closing sử dụng giãn nở trước rồi dùng xói mòn.
Với 2 tập điểm ảnh A và B, ký hiệu Closing: 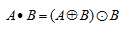
Closing có chức năng chính là lấp các khe hoặc các lỗ hổng giữa các điểm ảnh trên A. Khoảng cách lấp tùy theo kích thước và hình dạng của B.
Đầu tiên, thực hiện giãn nở giúp lấp hết các lỗ hổng hoặc khe hở trên A. Sau đó thực hiện xói mòn, thu được tập các điểm ảnh gồm A và 1 vài điểm ảnh do lấp các lỗ hổng hoặc khe hở mà không bị sói mòn đi.
Minh họa Closing như sau:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig27.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig27.png?w=736)
Hình 27: Closing
Một vài tính chất của Closing:
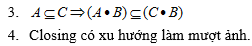
3.8. Ứng dụng khử nhiễu
Sử dụng Opening và Closing để khử nhiễu như sau. Giả sử có 1 ảnh nhị phân bị nhiễu, 1 vài điểm ảnh trắng bị đổi thành đen và ngược lại. Để khử nhiễu, ta thực hiện Closing và Openning như sau, với mặt nạ B cho trước:
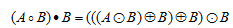
Cách này gọi là Morphological Filtering. Đầu tiên, 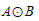 sẽ loại bỏ các điểm ảnh đen riêng biệt, tuy nhiên nó sẽ tạo ra các lỗ. Ta sẽ lấp các lỗ đó bằng cách giãn nở 2 lần. Lúc này, kích thước vật thể bị phình to ra nên ta cần xói mòn thêm 1 lần.
sẽ loại bỏ các điểm ảnh đen riêng biệt, tuy nhiên nó sẽ tạo ra các lỗ. Ta sẽ lấp các lỗ đó bằng cách giãn nở 2 lần. Lúc này, kích thước vật thể bị phình to ra nên ta cần xói mòn thêm 1 lần.
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig28.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig28.png?w=736)
Hình 28: Morphological Filtering
Khái niệm cơ bản về xử lý ảnh Computer Vision và các phép toán trong xử lý ảnh.
![]() Reviewed by Jacky
on
tháng 11 04, 2017
Rating:
Reviewed by Jacky
on
tháng 11 04, 2017
Rating:
![[20160624] TÀI LIỆU XỬ LÝ ẢNH CƠ BẢN-Sửa lần 5_Fig1.png](https://univtechnews.files.wordpress.com/2017/04/20160624-tc3a0i-lie1bb87u-xe1bbad-lc3bd-e1baa3nh-cc6a1-be1baa3n-se1bbada-le1baa7n-5_fig1.png?w=134)



Không có nhận xét nào: